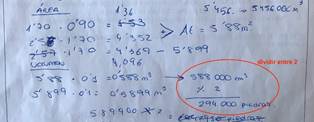Revista de Educación Mediática y TIC 2026, 15 (1). ISSN 2254-0095

EXPLORANDO RUTAS MATEMÁTICAS: INTEGRANDO EL ENTORNO URBANO EN LA FORMACIÓN DOCENTE A TRAVÉS DE MATHCITYMAP

EXPLORING MATHEMATICS TRAILS: INTEGRATING THE URBAN ENVIRONMENT INTO TEACHER TRAINING THROUGH MATHCITYMAP

Angélica Benito¹, Álvaro Nolla², Elena Sánchez González³ y Ariadna Gómezescobar⁴

¹https://orcid.org/0000-0001-8722-9518, Universidad Autónoma de Madrid (España), angelica.benito@uam.es

²https://orcid.org/0000-0002-7434-6958, Universidad Autónoma de Madrid (España), alvaro.nolla@uam.es

³https://orcid.org/0000-0003-0543-7407, Universidad a Distancia de Madrid (España), elena.sanchez.go@udima.es

⁴https://orcid.org/0000-0001-5104-6269, Universidad de Castilla La Mancha (España), ariadna.gomezescobar@uclm.es

Recibido: 20/01/2025         Aceptado: 16/06/2025         Publicado: 16/01/2026

Resumen: La Didáctica de las Matemáticas ha evolucionado recientemente en la formación del profesorado, desarrollando nuevas herramientas para dotar a los futuros docentes, variedad de estrategias de enseñanza. Una de estas herramientas es la utilización del entorno como recurso didáctico, haciendo que éste sirva como foco de formación para los estudiantes, aprovechando las Matemáticas presentes en el entorno urbano para vincular la matemática formal con la realidad cotidiana. Este trabajo propone las rutas matemáticas como recurso para la formación de futuros docentes de Grado en Maestro/a en Educación Infantil y Educación Primaria, lo que se materializa en la propuesta de una ruta matemática por la Universidad Autónoma de Madrid implementada con la aplicación móvil MathCityMap y accesible con el código del texto. La ruta matemática es vivenciada por 396 estudiantes de ambos grados. Durante su realización, cumplimentan el cuestionario de satisfacción SIMS. Los resultados indican puntuaciones favorables en el índice de Autodeterminación, y en las cuatro dimensiones que mide el cuestionario (Motivación Intrínseca, Regulación Identificada, Regulación Externa y Automotivación). Además, se describen y analizan las respuestas de tres tareas representativas, evidenciando algunos errores de concepto que tienen los estudiantes del Grado, pudiendo incidir en ellos, durante la docencia de la asignatura

Abstract: In the field of teacher education, Mathematics Didactics has evolved quite extensively in recent years, developing new tools to provide future teachers with a variety of teaching strategies. One of these tools is the use of the environment as a didactic resource, making it serve as a training focus for students and taking advantage of the mathematics found in any city to extrapolate formal mathematics to everyday life. This work proposes mathematics trails as a resource for the training of future teachers in Early Childhood and Primary Education, which is materialized in the proposal of a mathematics trail through the Universidad Autónoma de Madrid implemented with the MathCityMap mobile application and accessible with the text code. The mathematics trail is experienced by 396 students of the Bachelor's Degree in Early Childhood and Primary Education who, during its completion, complete the SIMS satisfaction questionnaire. The results indicate favorable scores in the four dimensions measured by the questionnaire (Intrinsic Motivation, Identified Regulation, Extrinsic Regulation, and Amotivation), as well as in the Self-Determination Index. In addition, three representative tasks are described, and the students' responses are analyzed, highlighting some concept errors that the undergraduate students have and that, therefore, should be addressed in the teaching of the subject.

Résumé: L'enseignement des mathématiques a récemment évolué dans la formation des enseignants, avec le développement de nouveaux outils permettant d'offrir aux futurs enseignants une variété de stratégies pédagogiques. L'un de ces outils est l'utilisation de l'environnement comme ressource pédagogique, le plaçant au cœur de la formation des élèves, exploitant les mathématiques présentes en milieu urbain pour relier les mathématiques formelles à la réalité quotidienne. Ce travail propose des parcours mathématiques comme ressource pour la formation des futurs enseignants de la licence en éducation préscolaire et primaire. Ceci se matérialise par la proposition d'un parcours mathématique à l'Université autonome de Madrid, mis en œuvre grâce à l'application mobile MathCityMap et accessible via le code dans le texte. Ce parcours a été suivi par 396 étudiants des deux filières. Lors de sa réalisation, ils ont rempli le questionnaire de satisfaction SIMS. Les résultats indiquent des scores favorables à l'indice d'autodétermination et aux quatre dimensions mesurées par le questionnaire (motivation intrinsèque, régulation identifiée, régulation externe et auto-motivation). De plus, les réponses à trois tâches représentatives sont décrites et analysées, mettant en évidence certaines idées fausses que les étudiants du diplôme ont, qui peuvent les influencer pendant l'enseignement de la matière.

Palabras Clave: Rutas matemáticas; Formación inicial del profesorado; TIC; MathCityMap

Key words: Math trails; Initial teacher training; ICT; MathCityMap

Mots clés: Parcours mathématiques; Formation initiale des enseignants; TIC; MathCityMap

INTRODUCCIÓN

Uno de los aspectos a destacar en el proceso de enseñanza-aprendizaje es el hecho de poder generar situaciones problemáticas donde los conocimientos matemáticos sirvan como respuesta a esa situación (De Castro et al., 2015). En este sentido, Edo (2000) enfatizaba la relevancia de diseñar excursiones educativas centradas en el ámbito de las Matemáticas dirigidas a estudiantes de segundo ciclo de Educación Infantil (3-6 años). Este enfoque busca que los niños vivencien y descubran conceptos matemáticos dentro de su entorno inmediato. Para llevar a cabo esta iniciativa, es imperativo que los docentes posean conocimientos sólidos, recursos adecuados y la habilidad para crear situaciones problemáticas que se ajusten a las capacidades de los alumnos en esta etapa de desarrollo. Por lo tanto, se destaca la necesidad de que las Facultades de Magisterio proporcionen herramientas formativas que faciliten la preparación y ejecución de estas actividades en el contexto educativo. Estas actividades, concretamente las rutas matemáticas, pueden ir dirigidas a todo tipo de público y etapa, desde edades tempranas, hasta público adulto.

Podría definirse una ruta matemática como una secuencia de paradas previamente diseñadas en la que se realizan actividades matemáticas basadas en el entorno (Cross, 1997). La tipología de estas actividades puede ser de naturaleza analítica, resolutiva o incluso de formulación de las propias tareas de la ruta (Shoaf et al., 2004). En cualquier caso, la clave está en que las tareas requieran algún tipo de interacción de la persona que hace la ruta con el entorno. Es esta interacción es precisamente lo que diferencia la tarea de una ruta de cualquier otro tipo de tarea que pueda ser llevada a cabo dentro del aula, donde por lo general, se trabaja con imágenes o información textual que no proponen tareas auténticas y realistas que requieran una modelización del problema a tratar (Jablonski et al., 2020).

Las rutas matemáticas tienen cabida en diversos contextos, tanto de divulgación, como para trabajar los contenidos del currículum en la docencia. Utilizar estas rutas para divulgación permite encontrar relaciones matemáticas en los objetos más inesperados y reflexionar sobre la importancia de las Matemáticas en la sociedad. Estos beneficios también se pueden disfrutar incorporando las rutas matemáticas en la actividad docente, integrando los contenidos del currículum en un contexto real, enriqueciendo las clases de Matemáticas y mostrando su utilidad (Navas, 2019). El hecho de analizar la ciudad donde se vive y conectar con sus detalles a través de una atmósfera de aventura y de exploración matemática, y tal vez también no matemática (interdisciplinar), supone una motivación hacia unas Matemáticas más significativas a través del aprendizaje y del disfrute.

La ejecución de una ruta matemática puede tener cabida en diversas etapas educativas.  En Educación Primaria se encuentran ejemplos en Ruíz y Garrido (2020), y Nolla y Benito (2020) en la ciudad de Madrid. Asimismo, en educación secundaria pueden encontrarse varias rutas en el monográfico Queralt Llopis (2020), etapa donde se observa como el uso de dispositivos móviles facilitó los procesos de enseñanza y aprendizaje de Matemáticas fuera del aula (Cahyono & Ludwig, 2019).

Con respecto al ámbito universitario y en relación con la formación de profesorado cabe destacar, por un lado, el proyecto conjunto entre profesorado en activo y futuros docentes sobre la creación y puesta en práctica de rutas matemáticas desarrollado por Moffet (2011), donde se observaron, en ambos colectivos, un positivo desarrollo en su confianza, competencia y motivación de cara a desarrollar futuras experiencias fuera del aula. Por otro lado, Barbosa y Vale (2020) proponen una ruta matemática mediante la aplicación MathCityMap a estudiantes de magisterio, quienes valoran positivamente la experiencia, destacando el poder resolver problemas realistas, el establecimiento de conexiones matemáticas, el pensamiento crítico y el trabajo cooperativo.

Aplicación MathCityMap

MathCityMap (MCM) es una plataforma a nivel mundial que permite crear, utilizar y compartir rutas matemáticas. Surge a partir del proyecto europeo ERASMUS+ Mobile Math Trails in Europe (MoMaTrE, http://momatre.eu) y su continuación Math Trails in School, Curriculum and Educational Environments of Europe (MaSCE3, https://masce.eu) y consta de un portal web (https://mathcitymap.eu/es/), orientado a la creación y seguimiento de rutas, y la aplicación para dispositivos móviles para la ejecución de las rutas.

Para crear una ruta desde el portal web es necesario proponer un mínimo de cuatro tareas o actividades matemáticas. Cada tarea deberá estar geolocalizada, contener una fotografía relacionada con la tarea a resolver, además pueden incorporarse pistas escalonadas y diferentes tipos de soluciones (numérica, intervalo, selección múltiple, espacios en blanco…). Las tareas pueden ser reutilizadas de las propuestas por otros usuarios, pues la plataforma cuenta con un proceso de control y revisión (Jablonski et al., 2020). Para asegurar la calidad de una tarea, Jablonski et al. (2018) proponen los siguientes criterios que deben cumplirse para que sea de acceso público: unicidad, presencia, participación, soluciones múltiples, realismo, ayudas escalonadas, etiquetas curriculares, formatos de las soluciones, herramientas y solución de muestra.

Otro aspecto importante en la creación de rutas es definir previamente el contenido matemático que se desea trabajar para elegir el tipo de preguntas que se han de formular, “hay que saber analizar si trabajar los conceptos que se encuentran por la calle o ir a las calles donde poder trabajarlos conceptos apropiados” (Vilches, 2020, p 36).

En cualquier caso, a la hora de diseñar la ruta, deben tenerse en cuenta los conocimientos matemáticos de los asistentes, los cuales serán más homogéneos al tratarse de alumnado de una clase y más heterogéneos si es público general el que asiste a una ruta de tipo divulgador.

Para la ejecución de la ruta, basta con introducir el código de la ruta en MCM y descargar la ruta. La aplicación muestra la propia ubicación y un mapa con la ruta de las tareas y la ubicación de cada una. Desde el Aula Digital de MCM, el docente puede hacer un seguimiento de la ubicación de cada estudiante, así como de sus respuestas. Mediante la integración del Sistema de Posicionamiento Global (GPS) en la aplicación educativa se posibilita la transmisión de mensajes en tiempo real dentro del grupo, así como la facilitación de consultas por parte de los estudiantes al docente a través del chat integrado en la aplicación. Las potencialidades de este recurso fueron impulsadas conforme a los resultados positivos de los estudios pioneros, como los llevados a cabo por Cahyono y Ludwig (2019), en donde subrayan el entusiasmo generado tanto en los docentes como en los estudiantes que participaron en dichos estudios piloto. Este entusiasmo ha demostrado mejorar las creencias de ambos agentes educativos en relación con las Matemáticas, teniendo un impacto positivo en la motivación intrínseca de los estudiantes para participar en actividades matemáticas (Cahyono, 2018), además de contribuir a la mejora de su competencia en esta disciplina.

Barbosa y Vale (2020) utilizan la aplicación MCM en su propuesta de ruta matemática y el alumnado evalúa la herramienta como fácil de usar y motivadora, considerando que contribuye al compromiso de los estudiantes a través de la participación activa.

Además, Hass et al. (2021), resaltan la influencia positiva de las rutas matemáticas digitales en el fomento del desarrollo de habilidades STEAM (Ciencia, Tecnología, Ingeniería, Artes y Matemáticas). En su investigación, subrayan el proceso mediante el cual los estudiantes de magisterio, bajo una formación previa, elaboraron propuestas colaborativas para integrar elementos de pintura, escultura, arquitectura y construcciones culturales dentro del ámbito de las Matemáticas, utilizando MCM. Enfatizan la interconexión entre los conceptos matemáticos del aula con el mundo real a través de la implementación de la tecnología educativa.

Por otro lado, Martínez-Jiménez et al. (2022) proporcionan futuras líneas de trabajo para abordar las dificultades que enfrentan los futuros docentes en el ámbito STEAM tras la puesta en marcha de una experiencia piloto con estudiantes de tercer curso de magisterio. Destacan su capacidad para generar situaciones en un contexto real. No obstante, se identificó que la mayoría de las tareas analizadas eran de naturaleza procedimental en lugar de abordar problemas de resolución, evidenciando una marcada falta de apertura, creatividad y exigencia cognitiva. Con el objetivo de subsanar estas deficiencias, se sugieren diversas estrategias. En primer lugar, se propone que los estudiantes experimenten un recorrido matemático predefinido, lo que implica una previa familiarización con la aplicación MathCityMap. Asimismo, se sugiere invitar a centros de educación Primaria permitiéndoles vivenciar los diseños elaborados por los estudiantes de magisterio. Este último paso tiene como finalidad proporcionar a los estudiantes una oportunidad de autoevaluación, facilitándoles la revisión y rediseño de sus propuestas. Además, se considera que este proceso de reflexión contribuirá significativamente a su preparación para la futura práctica profesional.

El proyecto de innovación MathCityM-ApS

Este trabajo está enmarcado en un proyecto de innovación, MathCityM-ApS, el cual surge para contribuir al esfuerzo institucional de la Universidad Autónoma de Madrid (UAM) con la promoción de la excelencia docente y la mejora continua de la enseñanza universitaria, en este caso y de manera específica, en lo que respecta a la educación universitaria de los futuros profesionales de la enseñanza de Matemáticas de las etapas de Educación Infantil, Educación Primaria y Educación Secundaria. El proyecto pretende mejorar la calidad de la enseñanza que realiza el profesorado implicado en las asignaturas con contenidos de Matemáticas de las titulaciones del Grado y Máster de la Facultad de Formación de Profesorado y Educación, a través de la implementación de rutas matemáticas, proporcionando a los futuros docentes los recursos y herramientas necesarias para su inclusión en actividades prácticas.

El alumnado de Grado y Máster de la Facultad de Formación del Profesorado y Educación recibe formación sobre las rutas matemáticas como recurso didáctico, sobre la implementación de las mismas con la aplicación móvil MathCityMap, el uso de Realidad Aumentada con GeoGebra RA y sobre la metodología Aprendizaje-Servicio. El alumnado primero realiza una ruta por el campus de la universidad, para ello, dependiendo de la titulación en la que están matriculados (Grado de Educación Infantil, Grado de Educación Primaria, Máster de Profesor de ESO o Máster de Didácticas Específicas) el equipo docente ha implementado distintas rutas/tareas. Tras la experimentación de las rutas, los estudiantes universitarios, teniendo en cuenta las consideraciones didácticas expuestas en las asignaturas relacionadas con Didáctica de Matemáticas, diseña en grupos su propia ruta matemática para que pueda ser puesta en práctica por alumnado real en un entorno real, ya sea en un centro escolar o cercano a él, o en el propio campus de la universidad.

Teniendo en cuenta todo lo anterior, los objetivos generales y específicos que persigue el proyecto de innovación MathCityM-ApS son los siguientes:

1. Crear nuevas herramientas o materiales docentes, para ser utilizados tanto en el aula como fuera de ella (formación presencial y no presencial).

1.1. Crear paseos matemáticos con MathCityMap para alumnado de los Grados de Maestro/a.

1.2. Crear paseos matemáticos con MathCityMap y Realidad Aumentada para alumnado del Máster de Formación del Profesorado de Secundaria y Bachillerato y el Máster en Innovación en Didácticas Específicas.

1.3. Vivenciar los paseos matemáticos con alumnado de Grado y Máster.

2. Diseñar e implementar de iniciativas innovadoras basadas en la metodología del Aprendizaje y Servicio (ApS).

2.1. Conocer la metodología ApS.

2.2. Experimentar la metodología ApS a través del diseño de paseos matemáticos para alumnado de Primaria e Infantil y su implementación con MathCityMap.

2.3. Evaluar las producciones propias y de los y las compañeras.

3. Identificar buenas prácticas en la docencia universitaria.

3.1. Fomentar disciplinas STEM a través de las TICs.

3.2. Usar lenguaje inclusivo en la propuesta de tareas para incluir así la perspectiva de género.

3.3. Reflexionar acerca de las buenas prácticas trabajadas a través del proyecto MathCityM-ApS.

MÉTODO/DESARROLLO DE LA EXPERIENCIA DE INNOVACIÓN

La Ruta Matemática por la universidad

En la primera parte del proyecto, el alumnado vivencia las rutas matemáticas diseñadas por el profesorado universitario. Estas rutas matemáticas se implementan mediante la aplicación MathCityMath (Figura 1), siguiendo los criterios de calidad referidos por Jablonski et al. (2018). La ruta matemática que se expone en el presente trabajo está ubicada en el campus de Cantoblanco de la Universidad Autónoma de Madrid y está disponible introduciendo en la aplicación móvil el código 014402. Consta de siete tareas, todas ellas relacionadas con contenidos del currículum de Educación Primaria (Tabla 1). El recorrido es de aproximadamente medio kilómetro a lo largo de la avenida principal de la universidad.

Figura 1. Ruta en la web de MathCityMap

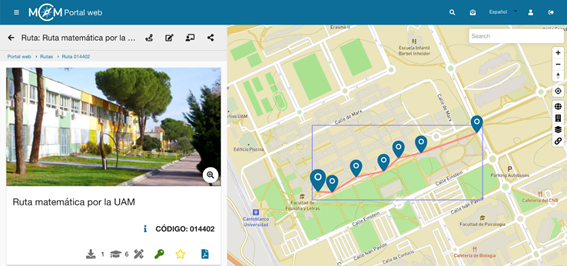
Este recorrido está diseñado para el alumnado de los primeros cursos de los Grados de Maestro/a, donde un alto porcentaje de estudiantes proviene de Ciclos Formativos o del Bachillerato de Humanidades. Por tanto, muchos de los participantes en la ruta llevan varios años sin enfrentarse a este tipo de problemas matemáticos. Por este motivo, en todas las tareas se incluyen pistas escalonadas para llegar a la solución. Estas pistas intentan evitar errores de medidas, conversiones de unidades, incluyen indicaciones de posibles estrategias y recuerdan algunas fórmulas que pueden usar. Los detalles específicos de cada tarea pueden consultarse en la sección “Descripción y análisis de tareas”.

Tabla 1. Tareas de la ruta matemática por la UAM. Fuente: Elaboración propia.

Nombre	Contenido	Objeto	Tarea
Contando los colores de la fachada	Proporción y porcentaje. Probabilidad.	Fachada del edificio	Calcular la proporción de pintura que se necesita para recubrir la parte de la fachada que es de color verde oscuro.
¿Cuántos cabemos en los bancos?	Número. Conteo. Medida.	Banco	Enumerar posibles estrategias que emplearía el alumnado de Infantil y Primaria para saber cuántos alumnos caben en un banco.
El arenero de Económicas	Geometría. Medida. Volumen del prisma.	Arenero	Hallar el número de piedras que caben en un arenero de base hexagonal.
La simetría de Tomás y Valiente	Geometría. Medida. Simetría.	Escultura	Determinar el área de aquellas planchas del suelo que en su conjunto poseen una simetría central.
Forrando el olivo de Ciencias	Geometría. Medida. Área de superficies.	Macetero	Calcular el área del papel necesario para recubrir un macetero de forma cilíndrica en el que no se puede medir el radio directamente.
Altura de la Plaza Mayor	Geometría. Medida. Triángulos. Thales.	Rampa	Estimar la altura de una rampa de grandes dimensiones.
Contando botones	Número. Conteo. Multiplicación.	Pavimento acera	Estimar el número total de botones de la zona embaldosada en un pavimento formado por baldosas con 9 botones.

Participantes

La ruta descrita anteriormente es ejecutada por un total de 369 estudiantes de primer curso de Grado en Maestro/a: 143 de Doble Grado (Infantil y Primaria), 126 de Grado en Maestro/a en Educación Infantil y 50 estudiantes matriculados/as en el Grado en Maestro/a en Educación Primaria.

Instrumento

A mitad de la ruta, se les envía un mensaje por la aplicación MathCityMap en la que se pide al alumnado que cumplimenten individualmente el cuestionario de motivación SIMS (Guay et al, 2000). Como indican los autores, los ítems del cuestionario se puntúan con una escala Likert de 1 a 7, siendo 1 “no se corresponde en absoluto” y 7 “se corresponde exactamente”. Estos ítems se pueden consultar en la Tabla 2 y componen las tres dimensiones de la motivación en función del nivel de autodeterminación al realizar la actividad:

Motivación Intrínseca (MI): relacionada con el hecho de realizar una actividad por el placer y motivación que provoca la misma. Esta dimensión se compone por los ítems 1, 5, 9 y 13.

Motivación Extrínseca (ME): referida a la realización de una actividad por los incentivos o consecuencias asociados a la misma. Esta dimensión se divide en otras dos:

1. Regulación Identificada (RI): cuando se adopta una conducta debido a su importancia para la consecución de los objetivos que se plantea el sujeto. En esta dimensión se tienen en cuenta los ítems 2, 6, 10 y 14.

2. Regulación Externa (RE): en este caso, la realización de la actividad está relacionada con el hecho de obtener una recompensa o evitar un castigo. Para el cálculo de esta dimensión se utilizan los ítems 3, 7, 11 y 15.

Amotivación (A): relacionada con la creencia de que la actividad no es importante, esto origina desmotivación y estaría directamente relacionada con ausencia de percepción entre la conducta que se adopta y sus consecuencias. Los ítems 4, 8, 12 y 6 conforman esta dimensión.

Como puede observarse, las dimensiones MI y RI tienen connotaciones positivas, mientras que RE y A serían dimensiones relacionadas con aspectos negativos. Guay et al. (2000) proponen también el Índice de Autodeterminación (IA), calculado como:

RESULTADOS

Descripción y análisis de tareas

A continuación, se han seleccionado tres tareas destacadas de la ruta, las cuales se describirán y se hará un breve análisis de las respuestas de los estudiantes.

El arenero de Económicas

En esta tarea el alumnado se encuentra con un arenero compuesto de dos partes rodeadas de unas tablas de madera (Figura 2): una parte cuadrada y otra hexagonal. El objetivo es que calculen cuántas piedras negras necesitan para rellenar la parte hexagonal, sabiendo que de media caben 2 piedras en 1 cm³, y que la altura del arenero es constante e igual a 10 cm.

Para resolver la tarea pueden seguir al menos dos estrategias para hallar el área de la base: descomponer el hexágono en dos rectángulos (como en la Figura 3 izquierda) o restarle al cuadrado grande la parte cuadrada y sus bordes.

Figura 2. Midiendo el arenero.

En general, bastantes estudiantes encontraron problemas a la hora de llegar a la solución. Principalmente debido a la falta de precisión en las medidas, que incluían los bordes de madera al medir (donde no caben piedras), al mal uso de las unidades (mezclando metros y centímetros), errores de conversión (al pasar de m³ a cm³) o una vez calculado el volumen, al pasar al número de piedras, dividían entre dos. Véase la Figura 3.

Figura 3. Detalle de algunas respuestas del Arenero de Económicas.

Forrando el olivo de Ciencias

El enunciado de la tarea versa así: “Observad el olivo que hay en frente de la entrada de la Facultad de Ciencias. Nos han pedido decorar el gran macetero del olivo y hemos decidido forrarlo con papel de color. ¿Qué superficie de papel necesitamos para forrar la parte exterior del macetero? Da el resultado en m².”

Se debe calcular el área lateral de un cilindro (Figura 4). El problema radica en que el olivo está en mitad del macetero, lo que hace que sea imposible medir el radio o el diámetro directamente. Como posibles estrategias para resolver este problema está el cálculo del perímetro midiéndolo a trozos o calcular el diámetro usando los adoquines paralelos del suelo.

Figura 4. Altura del macetero

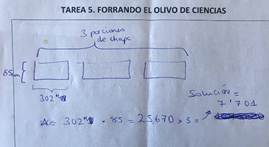
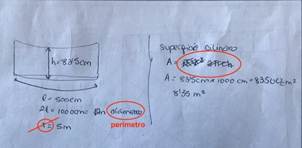
Las pistas introducidas en la aplicación guiaron a los grupos a recordar que el área lateral de un cilindro equivale al área del rectángulo cuya base es la longitud de la circunferencia de su base circular. Iniciaron distintas estrategias para medir el perímetro, entre ellas dividir la plancha metálica en tres (Figura 5 izquierda) o medirlo por completo. En algunos casos surgieron varios errores de concepto a la hora de interpretar la fórmula del área lateral del cilindro (Figura 5 derecha).

Figura 5. Detalle de algunas respuestas de Forrando el Olivo de Ciencias.

La altura de la Plaza Mayor

En esta tarea se pide calcular la altura de una rampa de grandes dimensiones (Figura 6). El objetivo es que se den cuenta de que la rampa y el suelo forman un triángulo y por tanto el cálculo de la altura se puede realizar a través del Teorema de Thales. El tramo ascendente de la rampa está dividido por 14 vallas equidistantes que permiten encontrar un triángulo semejante y más pequeño (medible) de manera sencilla.

Figura 6. La rampa y su altura.

En general, aunque el Teorema de Thales estaba incluido en las pistas, los grupos buscaron estrategias más directas para estimar esta altura: medir desde arriba lanzando una cinta métrica, usar una aplicación de medición del móvil, tomar una referencia (normalmente ellos mismos) y aproximar el número de veces que esa referencia completa la altura (Figura 7 izquierda). Otros asumieron que era un triángulo rectángulo e intentaron utilizar el Teorema de Pitágoras, aunque esta estrategia no solucionaba el problema de las grandes dimensiones.

Figura 7. Estrategia de estimación directa y una respuesta de la tarea Altura de la Plaza Mayor.

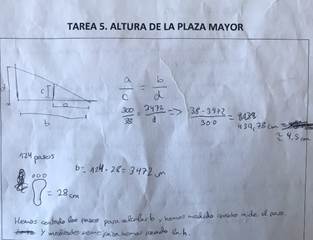
En la Figura 7 derecha se incluye la respuesta de uno de los grupos que utilizó el Teorema de Thales, al no tener cinta métrica, estimaron la longitud de la base usando la medida de un pie.

El equipo de docentes que acompañó al grupo durante el paseo recordó el enunciado del Teorema de Thales y cómo se podía resolver la tarea utilizándolo a aquellos grupos que resolvieron la tarea por estimación directa. Algunos de los grupos, por iniciativa propia, volvieron a calcular la altura de este modo para comprobar que ambas medidas eran similares.

Motivación frente a la ruta matemática

Durante la ejecución de las rutas, el alumnado cumplimentaba el cuestionario de motivación frente a la ruta matemática (SIMS). La Tabla 2 muestra las medias y desviaciones típicas para cada ítem, mientras que en la Tabla 3 pueden consultarse estos mismos datos para cada dimensión (Motivación Intrínseca, Regulación Identificada, Regulación Externa y Automotivación), así como para el Índice de Autodeterminación.

Tabla 2. Medias y desviaciones típicas para los ítems del SIMS. Fuente: elaboración propia.

Ítem         Cuestionario de motivación SIMS	Media	DT
1. Porque creo que esta actividad es interesante	5.51	1.69
2. Por mi propio bien	5.11	1.82
3. Porque se supone que debo hacerlo	4.31	2.09
4. Puede que haya buenas razones para realizar esta actividad, pero yo no veo ninguna	1.99	1.75
5. Porque disfruto con esta actividad	5.26	1.71
6. Porque creo que esta actividad es buena para mí	5.59	1.61
7. Porque es algo que tengo que hacer	4.33	2.09
8. Realizo esta actividad, pero no estoy seguro de si vale la pena	2.02	1.64
9. Porque esta actividad es divertida	5.40	1.76
10. Por decisión personal	4.16	2.13
11. Porque no tengo otra alternativa	2.72	2.01
12. No lo sé; no veo qué me aporta esta actividad	1.79	1.48
13. Porque me siento bien realizando esta actividad	5.13	1.83
14. Porque creo que esta actividad es importante para mí	5.36	1.68
15. Porque creo que tengo que hacerlo	4.19	2.16
16. Hago esta actividad, pero no estoy seguro de que sea conveniente continuar con ella	1.87	1.62

Tabla 3. Medias y desviaciones típicas para las cuatro dimensiones e índice de autodeterminación. Fuente: elaboración propia

Dimensiones e IA	Media	DT
Motivación Intrínseca (MI)	5.33	1.62
Regulación Identificada (RI)	5.06	1.50
Regulación Externa (RE)	3.89	1.70
Amotivación (A)	1.92	1.38
Índice de Autodeterminación (IA)	8.00	6.36

En las dimensiones con carácter positivo (MI y RI) se observan puntuaciones altas, mientras que las dimensiones relacionadas con aspectos negativos de la motivación (RE y A) las puntuaciones son más bajas. Las desviaciones típicas, por su parte, son similares y no destacables para las cuatro dimensiones. Los resultados de estas cuatro dimensiones se asemejan a los de Martínez-Jiménez et al. (2022) también con rutas matemáticas con estudiantes de Grado de Educación Primaria y a los de Cahyono et al. (2020) que, además de rutas, incorporan Realidad Aumentada para alumnado de Educación Secundaria.

Respecto al Índice de Autodeterminación (IA) de la muestra, se mueve en un rango entre -17 y 18, es decir, la muestra contiene estudiantes con índices extremos, a diferencia del estudio de Cahyono et al. (2020) que se mueve entre 1 y 14, y el de Martínez-Jiménez et al. (2022) entre -3.25 y 18. Sin embargo, la mayor parte de la muestra tiene un IA positivo, con una media de 8.

DISCUSIÓN/CONCLUSIONES

El presente trabajo muestra el diseño y desarrollo de una ruta matemática orientada al alumnado de Grado de Educación Infantil y Primaria implementada mediante la aplicación MathCityMap, dentro de un proyecto de innovación docente, MathCityM-ApS. En el texto, se proporciona una visión generalizada de las tareas de la ruta y se ahonda en tres de ellas, especificando su enunciado, imágenes asociadas y analizando brevemente algunas de las respuestas realizadas para la resolución de dichas tareas. Además, se proporciona el código de la ruta para su consulta y posible desarrollo de ésta con alumnado de Educación Secundaria, Bachillerato, Grado o Máster.

En el diseño de la ruta, aparte de los criterios de calidad para la elaboración de las tareas (Jablonski et al., 2018), se tuvieron en cuenta los contenidos a desarrollar durante las asignaturas de Grado relacionadas con la Didáctica de las Matemáticas, enriqueciendo así la parte matemática que este alumnado debe conocer (Navas, 2019).

Durante la ruta, el alumnado interactuaba con el entorno y manifestaba informalmente su satisfacción y motivación hacia la tarea propuesta. El grado de satisfacción y motivación se corrobora con las puntuaciones positivas obtenidas en el SIMS.

Otro de los aspectos clave de la vivencia de la ruta matemática por parte de estos futuros docentes es la propuesta de que sean ellos y ellas quienes, combinando el resto de conocimiento adquirido durante el curso académico, realicen una ruta matemática para sus futuros estudiantes (Navas, 2019). De esta manera, como indican Barbosa y Vale (2016), podría determinarse la capacidad del alumnado de Grado para identificar contextos reales y ricos que contribuyeran a plantear y resolver problemas que pudieran ser utilizados con alumnado de Educación Infantil y Primaria. Puede que la previa experimentación y el posterior diseño de rutas matemáticas incite a utilizar este recurso en su futura práctica docente.

REFERENCIAS

Alsina, Á. (2012). Hacia un enfoque globalizado de la educación matemática en las primeras edades. Números. Revista de didáctica de las matemáticas, 80, 7-24.

AlsinA, Á. (2019). La educación matemática infantil en España: ¿qué falta por hacer? Números: Revista Didáctica De Las Matemáticas, 100, 187-192.

Barbosa, A., & Vale, I. (2020). Math Trails through Digital Technology: An Experience with Pre-Service Teachers. In M. Ludwig, S. Jablonski, A. Caldeira, & A. Moura (Eds.), Research on Outdoor STEM Education in the digiTal Age. Proceedings of the ROSETA Online Conference in June 2020 (pp. 47-54). Münster: WTM.

Barbosa, A., & Vale, I (2016). Math trails: Meaningful mathematics outside the classroom with pre-service teachers. Journal of the European Teacher Education Network, 11, 63-72.

Cahyono, A. N. (2018). Learning Mathematics in a Mobile App-Supported Math Trail Environment. Cham (Switzerland): Springer International Publishing.

Cahyono, A. N., & Ludwig, M. (2019). Teaching and Learning Mathematics around the City Supported by the Use of Digital Technology. Eurasia Journal of Mathematics, Science And Tech. Education, 15(1), 1-8. Https://Doi.Org/10.29333/Ejmste/99514

Cahyono, A.N., Sukestiyarno, Y.L., Asikin, M., Miftahudin, Ahsan, M.G.K., & Ludwig, M. (2020). Learning Mathematical Modelling with Augmented Reality Mobile Math Trails Program: How Can It Work? Journal on Mathematics Education, 11(2), 181-192. http://doi.org/10.22342/jme.11.2.10729.181-192

Castro Hernández, C. D., Ruiz Olarría, A., Ruiz López, N., & Sáenz De Castro, C. (2015). Situaciones didácticas para el aprendizaje de las matemáticas en la educación infantil. Didácticas Específicas, 13.

Cross, R. (1997). Developing Maths Trails. Mathematics Teaching, 158, 38–39.

Edo, M. (2000). Mundo Matemático. Formas en el espacio. En M. Antón, B. Moll, (Eds.), Educación infantil. Orientación y recursos (0-6 años) (pp. 301-409). Barcelona: Praxis.

Guay, F., Vallerand, R. J., & Blanchard, C. (2000). On the assessment of situational intrinsic and extrinsic motivation: The Situational Motivation Scale (SIMS). Motivation and emotion, 24, 175-213 https://doi.org/10.1023/A:1005614228250

Haas, B., Kreis, Y., & Lavicza, Z. (2021). Integrated STEAM Approach in Outdoor Trails with Elementary School Pre-service Teachers. Educational Technology & Society, 24(4), 205-219 https://doi.org/10.30191/ETS.202110_24(4).0016

Jablonski, S., Lázaro, C., Ludwig, M., & Muñiz, T. J. R. (2020). MathCityMap, paseos matemáticos a través de dispositivos móviles. Uno: Revista de didáctica de las matemáticas, 87, 47-54.

Jablonski, S., Ludwig, M., & Zender, J. (2018). Task quality vs. task quantity. A dialog-based review system to ensure a certain quality of tasks the MathCityMap web community. Hans-Georg Weigand, Alison Clark-Wilson, Ana Donevska (Eds). Proceedings of the Fifth ERME Topic Conference (ETC 5) on Mathematics Education in the Digital Age (MEDA) (Pp. 115-122). Copenhague

Martínez-Jiménez, E.,Nolla De Celis, Á., & Fernández-Ahumada, E. (2022). The City as a Tool for STEAM Education: Problem-Posing in the Context of Math Trails. Mathematics, 10, 2995. https://doi.org/10.3390/math10162995

Martínez-Jimenez, E., Benito, A.,& Nolla A. (2022) Analysis of Motivations and Experiences of Elementary Education Teacher Training in Gamified Math Trails. Handbook of Research on International Approaches and Practices for Gamifying Mathematics. IGI Global Publisher of Timeline Knowledge. 2022. 10.4018/978-1-7998-9660-9

Moffet, P. V. (2011). Outdoor mathematics trails: an evaluation of one training partnership. International Journal of Primary, Elementary and Early Years Education, 39(3): 277-287. https://doi.org/10.1080/03004270903508462

Navas, J. (2019). Seminario federal: paseos matemáticos. SUMA, 90, 119-125.

Nolla De Celis, A., &Benito Sualdea, A. (2020). Matemáticas alrededor de las torres del norte de Madrid. En Pastor Blázquez, Mª M. & Santisteban Cimarro, A. (Coords.), Didácticas Específicas aplicadas a través del Patrimonio Local (pp. 495-523). Madrid: Paraninfo Universidad.

Ruíz López, N., & Garrido Martos, R. (2020). Recorridos matemáticos por la ciudad. En Pastor Blázquez, Mª M. y Santisteban Cimarro, A. (Coords.) Didácticas Específicas aplicadas a través del Patrimonio Local (pp. 461-480). Madrid: Paraninfo Universidad.

Shoaf, M.M., Pollak, H.O., & Schneider, J. (2004). Math Trails. Lexington, MA. Comap.

Vilches, S. (2020). Elefantes, estrellas, baldosas y rotondas. Estrategias para la autorregulación del aprendizaje. Uno: Revista de didáctica de las matemáticas, (87), 31-37.

Queralt Llopis, T. (2020). Monografía: rutas y paseos matemáticos. Uno: Revista de didáctica de las matemáticas, 87, 4-46.

Wijers, M., Jonker, V., & Drijvers, P. (2010). MobileMath: Exploring mathematics outside the classroom. ZDM Mathematics Education, 42, 789–799 https://doi.org/10.1007/s11858-010-0276-3

Contribución de los autores

Álvaro Nolla y Ariadna Gómezescobar coordinaron el proyecto y supervisaron la investigación. Angélica Benito y Álvaro Nolla diseñaron las tareas de la ruta matemática. Angélica Benito, Álvaro Nolla y Ariadna Gómezescobar, llevaron a cabo la implementación práctica de la ruta matemática y el análisis de los resultados obtenidos. Elena Sánchez González colaboró en la elaboración y revisión del marco teórico del estudio.

Financiación

Este estudio ha sido financiado por el proyecto de innovación docente “Paseos matemáticos con MathCityMap mediante Aprendizaje-Servicio en la Formación Inicial del Profesorado (MathCityMApS) - (FPYE_019.21_INN)”, subvencionado por el Vicerrectorado de Calidad de los Estudios e Innovación Docente de la Universidad Autónoma de Madrid.

Agradecimientos

Agradecemos al Grupo de Investigación sobre Educación Científica y Matemática en la Sociedad (GIECMES) de la Universidad Autónoma de Madrid por su respaldo académico en el desarrollo de esta experiencia.

Conflicto de intereses

Las autoras declaran no tener ningún conflicto de intereses.

Declaración de uso de la IA para la redacción del manuscrito

Las autoras declaran no haber empleado la IA para la redacción total o parcial de este manuscrito

Citación: Benito, A., Nolla, Á., Sánchez González, E. & Gómezescobar, A (2026). Explorando rutas matemáticas: integrando el entorno urbano en la formación docente a través de Mathcitymap. EDMETIC, Revista de Educación Mediática y TIC, 15(1), art.2. https://doi.org/10.21071/edmetic. v15i1.17913